Часто требуется перейти от одной системы координат (datum) к другой. Например, вы хотите данные с GPS в системе координат WGS84 наложить на карту в системе координат Пулково 1942 г.

Произодить преобразование проще (математически), если сначала перевести координаты из географических (широта и долгота) в прямоугольные (XYZ).

Чтобы получить точные прямоугольные координаты точки на поверхности Земли, необходимо знать не только широту и долготу, но и ее высоту над поверхностью эллипсоида. GPS показывает высоту над эллипсоидом WGS84. Можно вычислить прямоугольные координаты только по широте и долготе, считая, что точка лежит на поверхности эллипсоида, но при этом точность понизится.

Высоту точки на другими эллипсоидами получить сложнее. Обычно мы знаем высоту в национальной системе высот. За нулевую высоту, как правило, принимается среднее значение уровня моря в определенной точке побережья по результатам многолетних наблюдений. Высоты в этой системе измеряются геодезическими методами относительно поверхности геоида. Поэтому, чтобы узнать высоту точки над эллипсоидом, нужно знать возвышение геоида над эллипсоидом в данном месте, которое трудно вычислить с хорошей точностью. Существуют различные математические модели геоида для разных территорий и для всего земного шара, которые постоянно уточняются.

На заре спутниковой геодезии, когда взаимосвязи между системами координат не были четко определены, а данные исследований были не очень точны, применяли простой сдвиг начала координат dX, dY, dZ для перехода от одной системы координат к другой. Это предполагало, что направления осей двух эллипсоидов параллельны (что во многих случаях не соответствует действительности). Для работ на небольшой территории погрешности, вносимые этим предположением, были меньше, чем точность самих данных. Однако, по мере накопления и уточнения данных и повышения точности измерений, стало очевидно, что преобразование по трем параметрам не подходит для больших территорий и глобального использования, если требуется максимальная точность и единый набор параметров преобразования.

Простейший метод — сдвиг центра координат прямоугольной системы, предполагая, что оси исходной и целевой систем координат параллельны.

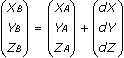
Молоденский разработал формулы для применения параметров сдвига к географическим координатам.

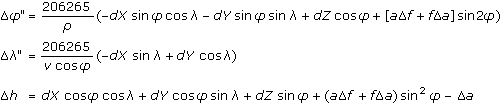
здесь dX, dY, dZ — сдвиг по осям, м;
a и f — большая полуось и сжатие исходного эллипсоида;
da и df — разности между большой полуосью и сжатием исходного эллипсоида и целевого эллипсоида.

Повышенная точность достигается преобразованием Хелмерта с 7-ю параметрами. Есть две его разновидности, различающиеся присвоением знака для параметров поворота.

1. Position Vector Transformation (Bursa-Wolf)

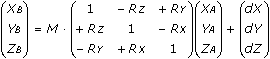
2. Coordinate Frame Transformation

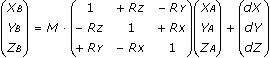
Здесь M — это масштаб (scale), параметры берутся из описания системы координат.